Das lange Kabel (2) – Leitungsbeläge
by Dr. Stack van Hay | 3. März 2013 02:44
Messung der Induktivität mit Funktionsgenerator und Oszilloskop
Mit der folgenden Versuchsanordnung habe ich versucht die Induktivität des Kabels grob abzuschätzen:
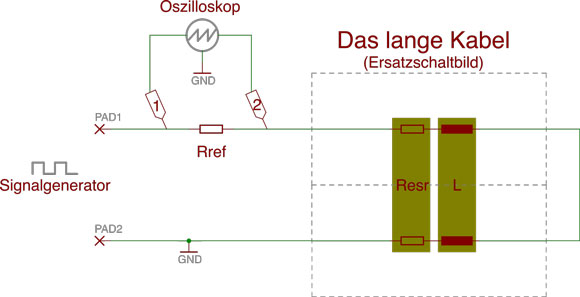
Versuchsanordnung zur Messung der Induktivität
[attention]Aber Achtung: Ein kleiner Denkfehler hat große Wirkung! Dadurch, dass ich Hin- und Rückleitung benutzt habe, bekomme ich es natürlich mit einer parasitären Kapazität zu tun (3 nF), die das Ergebnis ganz ordentlich verfälscht. Ursprünglich habe ich die Kapazität einfach ignoriert, dann habe ich in einer zweiten Version dieses Artikels die Messanordnung verändert. In der vorliegenden (dritten) Fassung habe ich einfach die Kapazität mit in die Auswertung genommen. [/attention]
Messprinzip
Der Referenzwiderstand bildet zusammen mit dem Widerstand der Leitung einen Spannungsteiler. Der Spannungsabfall an der Induktivität (dem Kabel) wird um so größer, je höher deren Widerstand ist, dieser Widerstand ist aber frequenzabhängig, je höher die Frequenz, desto höher der Wechselstrom-Widerstand des Kabels (der Induktivität).
Ich stelle die Frequenz so ein, dass ungefähr die Hälfte der Spannung am Referenzwiderstand abfällt, und die Hälfte am Kabel. Das Verfahren setzt natürlich voraus, dass keine Kapazitäten die Messung verfälschen, und dass der Referenzwiderstand weitgehend frequenzunabhängig ist.
Der Referenzwiderstand dürfte bei der verwendeten Frequenz von 80 kHz noch perfekt in Ordnung sein. Was die Kapazitäten angeht, so habe ich 3.92 nF gemessen, das ist 3 Größenordnungen kleiner, als die Induktivität, die bei Messung herauskommt, ich gehe also davon aus, dass sie das Messergebnis nicht über die Maßen beeinflusst.
Die Berechnungen sind eigentlich recht übersichtlich, da es um die Induktivität geht, muss ich natürlich vektoriell rechnen.
[latexpage]
Der Betrag der Impedanz $\left| Z \right|$ ergibt sich geometrisch zu:
\begin{align}
\left| Z \right|=\frac{\text{R}_{\text{ref}} \text{U}_{\text{1}}}{\sqrt{+\text{U}_{\text{1}}^2 – 2 \text{U}_{\text{1}} \text{U}_{\text{2}} \cos (\theta)+\text{U}_{\text{2}}^2}}
\end{align}
Der Winkel $\alpha$ entsprechend zu
\begin{align}
\alpha=\theta -\tan ^{-1}\left(-\frac{\text{U}_{\text{2}} \sin (\theta)}{\text{U}_{\text{2}}-\text{U}_{\text{2}} \cos (\theta)}\right)
\end{align}
Mit diesen beiden Zwischenergebnissen kann man aus den komplexen Formeln für die Impedanz
\begin{align}
Z=\text{R}_{\text{esr}}+i 2 \pi \text{f} \text{L}-\frac{i}{2 \pi \text{f} \text{C}}
\end{align}
und
\begin{align}
Z=\left| Z \right| \cos ( \alpha ) + i \left| Z \right| \sin (\alpha)
\end{align}
Schließlich $\text{L}$ zu
\begin{align}
\text{L} = \frac{-1+2\pi\ \text{C}\ \text{f}\ \left| Z \right| \sin ( \alpha )}{4 \pi^{2}\ \text{f}^{2}\ \text{C} }
\end{align}
und $\text{R}_{\text{esr}}$ zu
\begin{align}
\text{R}_{\text{esr}} = \left| Z \right| \cos ( \alpha )
\end{align}
berechnen.
Auswertung der Messung
Mit den Daten aus meiner Messung und dem Referenzwiderstand von 15 Ω:
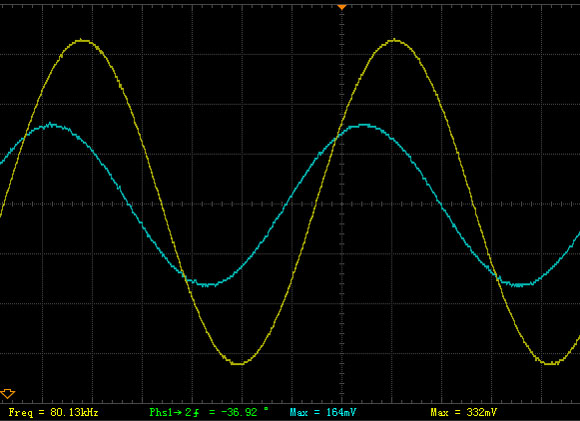 [1]
[1]$\text{R}_{\text{ref}}=15 \ \Omega$, $\text{f}=80 \ \text{kHz}$, $\theta=-36.92\ ^\circ$, $\text{U}_{\text{1}}=0.332 \ \text{V}$, $\text{U}_{\text{2}}=0.164 \ \text{V}$
Ergibt sich:
\begin{align}
\text{L} = 1\ \text{mH}
\end{align}
und
\begin{align}
\text{R}_{\text{esr}} = 4.9\ \Omega
\end{align}
Weitere Messdaten
Die Abschirmung hat in eine Richtung einen rein ohmschen Widerstand von: 3,08 Ω
Eine Einzelader hat in eine Richtung einen rein ohmschen Widerstand von: 2,00 Ω
Die Kapazität zwischen zwei Einzeladern beträgt: 3,92 nF
Fazit
1 mH erscheint mir sehr viel!
- [Image]: /wp-content/uploads/2013/03/InduktivitaetMessung.jpg
Source URL: https://drsvanhay.de/lange-leitung-induktivitat/