Gadget Inspektor:
Rigol DS2202 Fourier Transformation (Video)
by Dr. Stack van Hay | 25. April 2013 13:40
[latexpage]Die Fourier Transformation der Rigol DS 2000er im Video, mit einigen Erläuterungen im Text.
Kein Spektrum Analysator
Natürlich ist ein Oszilloskop kein Spektrum-Analysator und deswegen kann auch die Fourier-Transformations-Funktion eines Oszilloskopes nicht alles bieten, was man sich wünschen würde.
Konkret fehlen der eingebauten Fourier Transformation der Rigol 2000er einige Features, die vielleicht recht nett wären:
- Keine Fourier Transformation mehrerer Kanäle gleichzeitig
- Keine Fourier Transformation eines ausgeschalteten Kanals
- Keine Glättung der Fourier Transformation
- Keine logarithmische Skalierung der Frequenzachse (sehr wohl aber der Signalachse!)
Technische Daten
Die vielleicht wichtigste Frage lautet doch bestimmt: Wie viele Punkte gehen überhaupt in die Fourier Transformation ein?
Zunächst: Speichertiefe und Sample-Rate haben keine direkte Auswirkung auf die Fourier Transformation. Die Fourier Transformation basiert immer auf exakt 1400 Punkten (ja genau! Keine 2er Potenz, also eigentlich wohl eher DFT) und diese 1400 Punkte stammen immer aus dem sichtbaren Bereich der Messkurve. Dadurch sind Frequenz und Auflösung der Fourier Transformation dann auch geklärt:
Frequenz-Limit
Mit einer Auflösung der Zeitachse (Zeit pro Division) von $t_{D}$ ergibt sich eine maximale Frequenz von (Rigol schneidet 20% an dem Ende mit den hohen Frequenzen weg):
\begin{align}
f_{max} = \frac{40}{t_{d}}
\end{align}
[toggle title=“Herleitung“ style=“fancy“]
\begin{align}
f_{sample} = \frac{1400 \ Sa}{t_{d} \cdot 14 \ Divisions}
\end{align}
\begin{align}
f_{max} = \frac{1}{2} f_{sample} * \frac{4}{5} = \frac{40}{t_{d}}
\end{align}
[/toggle]
Auflösung
Für die Auflösung ergibt sich durch die verbleibenden 560 Fourier Transformation-Punkte:
\begin{align}
f_{Auflösung} = \frac{f_{max}}{560 \ \cdot \ t_{D}} = \frac{1}{t_{D} \cdot 14}
\end{align}
Beispiel für Auflösungen und maximale Frequenzen:
Zeitachse maximale Frequenz Auflösung 1 s/Div 40 Hz 0.07 Hz 1 ms/Div 40 kHz 0.07 kHz 1 µs/Div 40 MHz 0.07 MHz
Das Video
Die Beispiele aus dem Video
- Normaler Sinus mit 10 kHz.
- alternierendes Signal mit 5 bzw. 3 Frequenzanteilen.
- Amplitudenmodulierter Sinus 10 kHz mit 1 kHz moduliert.
- Quarzoszillator mit 16 MHz.
- Amplitudenmodulierter Sinus 2 MHz mit 20 kHz moduliert.
Das alternierende Signal (Details)
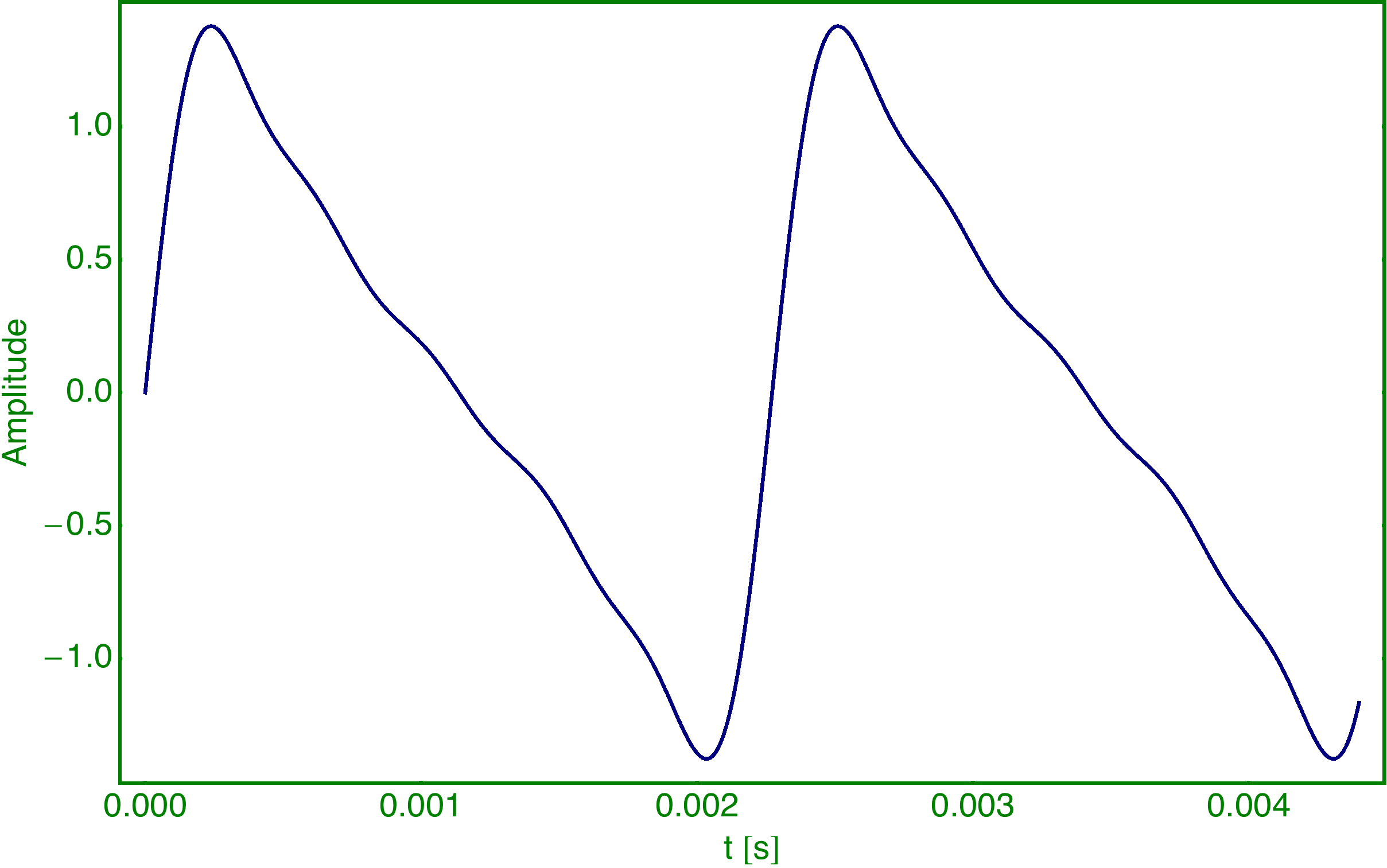
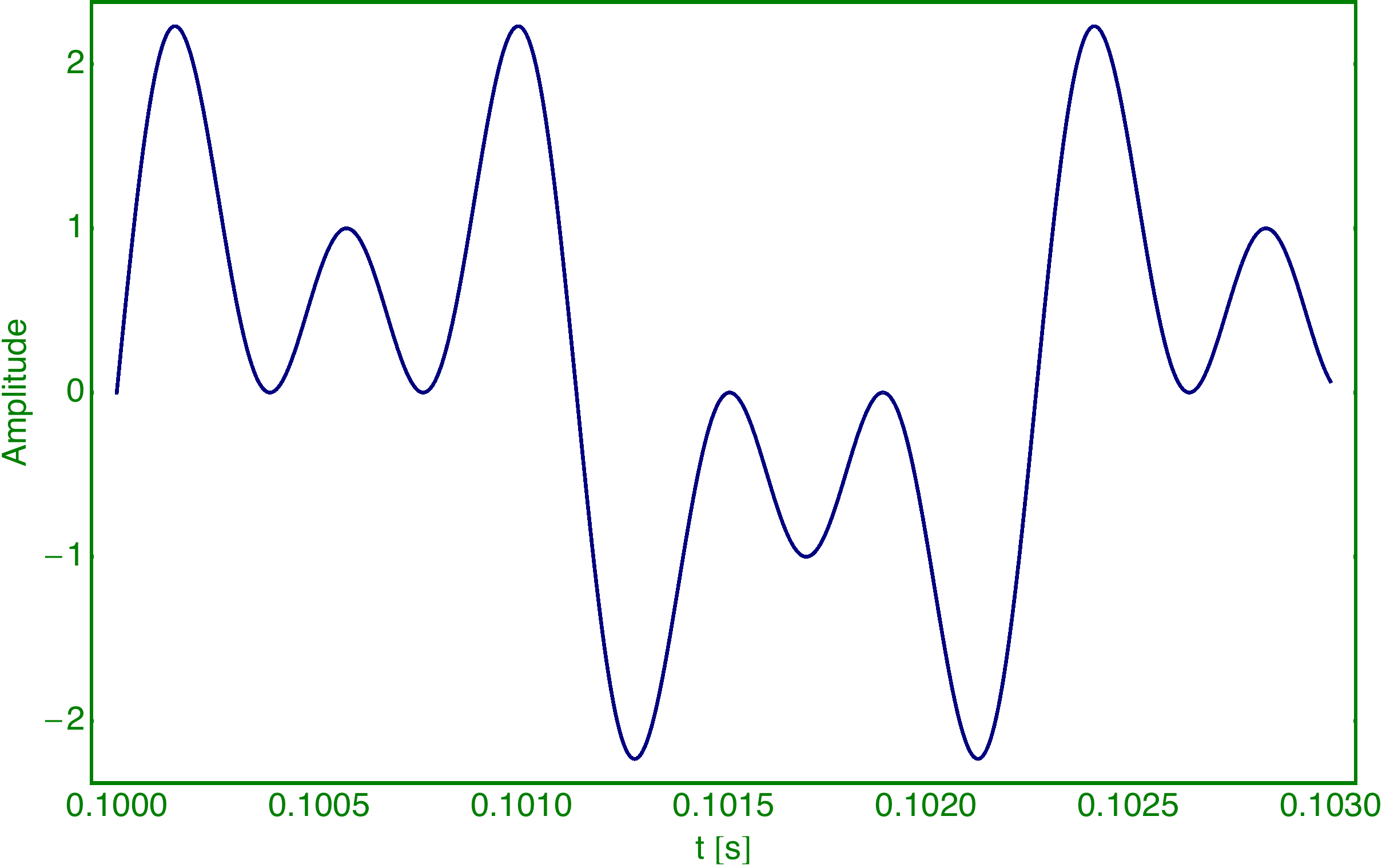
Das Signal besteht aus zwei Komponenten, die sich alle 0.1 s abwechseln:
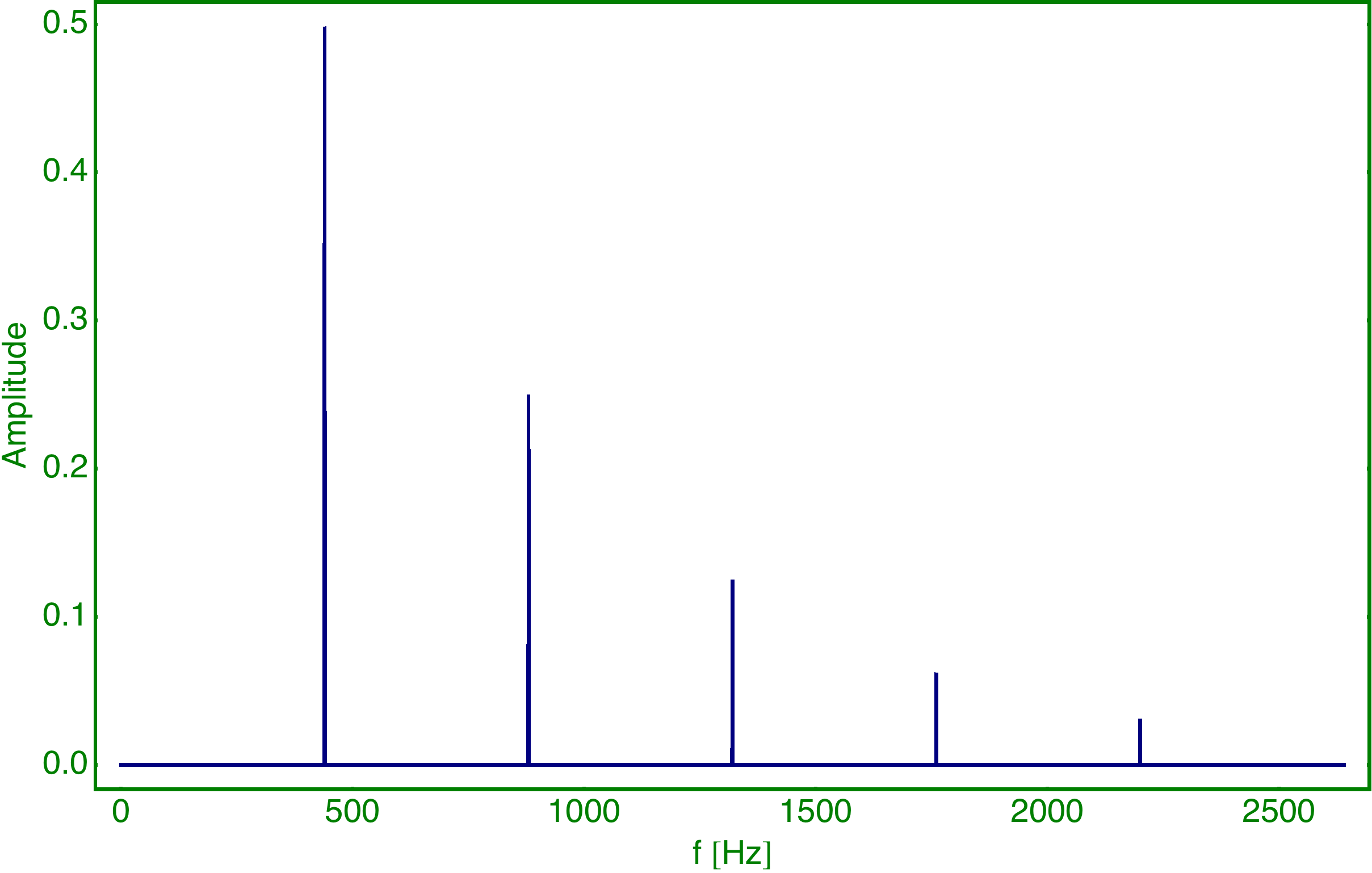
Komponente 1 sieht einem Sägezahn ähnlich und besteht aus: Index Frequenz Amplitude 1 440 Hz 16 2 880 Hz 8 3 1320 Hz 4 4 1760 Hz 2 5 2200 Hz 1
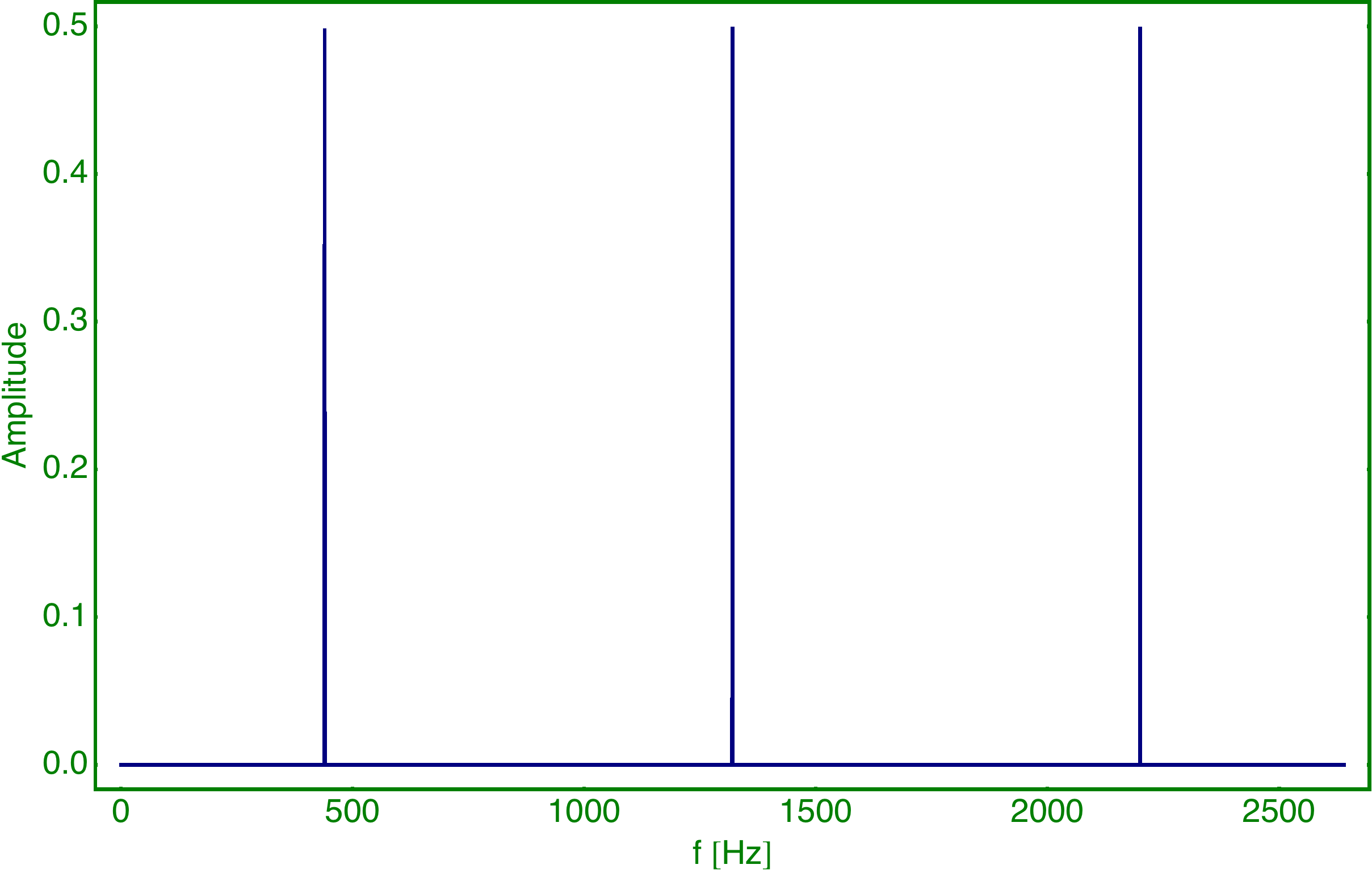
Bei Komponente 2 fehlen die Frequenzen mit den geraden Indizes und alle Amplituden sind gleich groß: Index Frequenz Amplitude 1 440 64 3 1320 64 5 2200 64
Source URL: https://drsvanhay.de/gadjet-inspektorrigol-ds2202-fft-video/