Das lange Kabel (3) – Länge

by Dr. Stack van Hay | 6. März 2013 02:27

Aus den bisherigen Messungen sollte ich eigentlich ausrechnen können, wie lang das Kabel eigentlich ist.

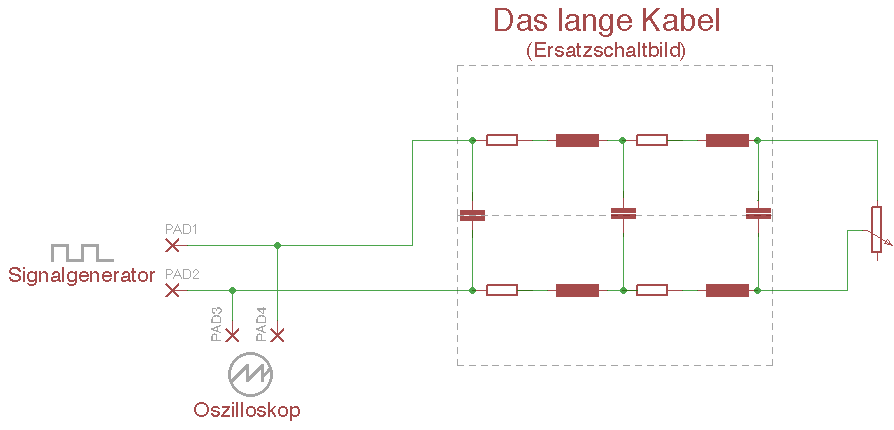
Wenn ich mir den Schaltplan der Versuchsanordnung in Das lange Kabel (1)[1] noch mal ansehe

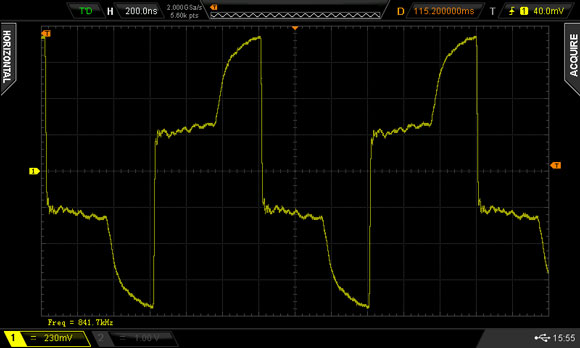
Dann wird mir klar, warum die Messung so aussieht, wie sie aussieht und wie ich aus dem Signal die Leitungslänge berechnen kann: Der Impuls des Signalgenerators (vergleiche auch das Originalsignal) erreicht die Stelle wo Signalgenerator, Tastkopf und „Das lange Kabel” miteinander verbunden sind. Durch die Anwesenheit des langen Kabels ist der Signalpegel jetzt geringer als ohne das lange Kabel, denn ein Teil des Signals läuft in das lange Kabel und nur ein verringerter Anteil läuft in den Tastkopf des Oszilloskopes und wird gemessen.

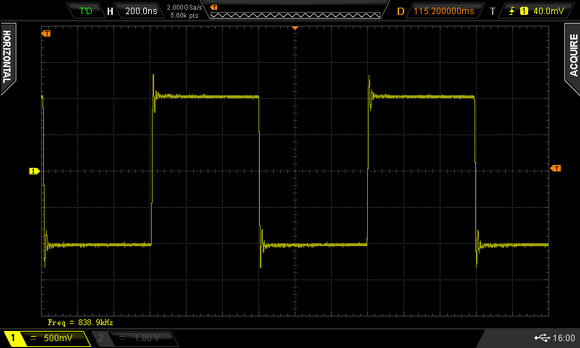
Nach einer bestimmten Zeit wird das Signal am Leitungsende reflektiert und kommt zurück zu der Verbindungsstelle. Wenn das schnell genug geht, überlagert es sich dabei mit dem Signal des Signalgenerators und es kommt zur Messung eines starken Signalanstieges, der sogar den Pegel des Originalsignales übersteigen kann.

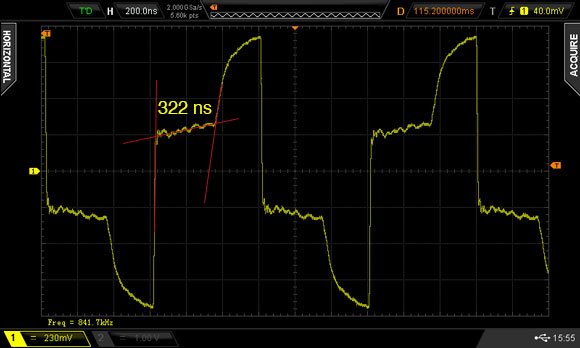
Aus der Dauer des reduzierten Pegels müsste ich also ausrechnen können, wie lang das Kabel eigentlich ist.

[3]

Die Dauer des verzögerten Signalanstieges beträgt

[latexpage]

\begin{align}
\Delta t = 322\ \text{ns}
\end{align}

Das Signal wandert in dem Kabel mit einer Geschwindigkeit etwa in Höhe der Vakuumlichtgeschwindigkeit $c$

\begin{align}
\text{v} = \text{vf} \cdot \text{c}
\end{align}

Der Velocity-Faktor $\text{vf}$ kommt daher, dass die Welle (das Feld) sich eben nicht im Vakuum ausbreitet, sondern auf zwei Leitern mit Dielektrikum dazwischen. Der Velocity-Faktor hängt also von der Permeabilität[4] und der Permittivität[5] ab, oder anders ausgedrückt, von der Einheitsinduktivität und der Einheitskapazität. Ich habe im Internet Werte für den Velocity-Faktor von 0.4 bis 0.8 gefunden. Für viele Kabel mit kompakten Dielektrika wird wohl gerne ein Wert von 0.66 angenommen. Mit dem rechne ich weiter.

Es ergibt sich also schließlich für die Länge $l$ des Kabels:

\begin{align}
\text{l} =\frac{1}{2} \text{vf} \cdot \text{c} \cdot \Delta \text{t} =\frac{1}{2} 0.66 \cdot 299792458\ \text{m/s} \cdot 322\ \text{ns} = 32\ \text{m}
\end{align}

Das Kabel müsste also nach Auswertung der Signalverformung so etwa um die 32 m lang sein, mit etwa Spielraum, weil der Velocity-Faktor von 0.66 ja nur geraten ist und nicht unbedingt für das vorliegende TQ-Kabel gelten muss.

Zum Folgenden Abschnitt bitte den Kommentar von Martin Schönegg beachten!
Ich habe also auch mit einem Lineal nachgemessen, und erhalte: 33.80 m, nicht schlecht, finde ich! Wie gut das genau ist, muss ich noch überprüfen, denn die Länge, die ich über die Wellenreflexion gemessen habe, ist natürlich die Länge der Adern, nicht die des Kabels. Die Adern sind aber gewunden (twistet) also muss die elektrisch bestimmte Länge schon mal länger sein, als die mechanisch bestimmte Länge.

Source URL: https://drsvanhay.de/das-lange-kabel-3-wie-lang-ist-es-eigentlich/

---