Bildschirmfoto ➟ CSV

by Dr. Stack van Hay | 26. Juli 2013 11:58

Ich habe im Internet ein Foto von einem Kurvenverlauf gefunden und wollte diesen Kurvenverlauf gern digitalisieren um ihn mit meinem Funktionsgenerator nachzuahmen. Ich habe das mit Mathematica gemacht.

Das Ausgangsfoto

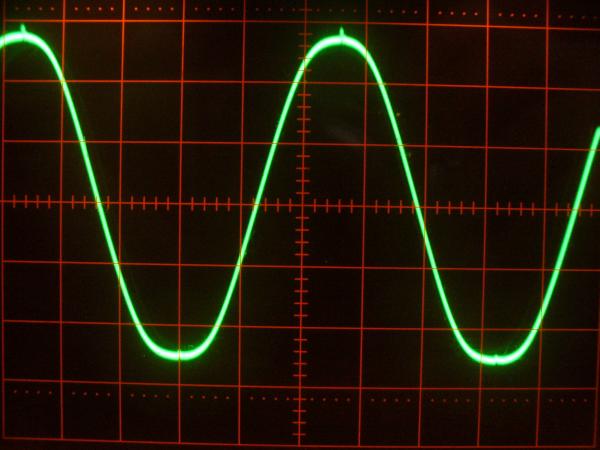
Zeigt eine von einem selbstgebauten Funktionsgenerator erzeugte Sinuskurve, gemessen mit einem analogen Oszilloskop. Für mein Experiment ist das Foto gut geeignet, weil es natürlich nicht extra zum Digitalisieren erzeugt wurde und weil es mit seinem kleinen Peak oben auf der Sinuskurve auch gleich noch einen guten Testfall enthält.

Schritt für Schritt

Freistellen

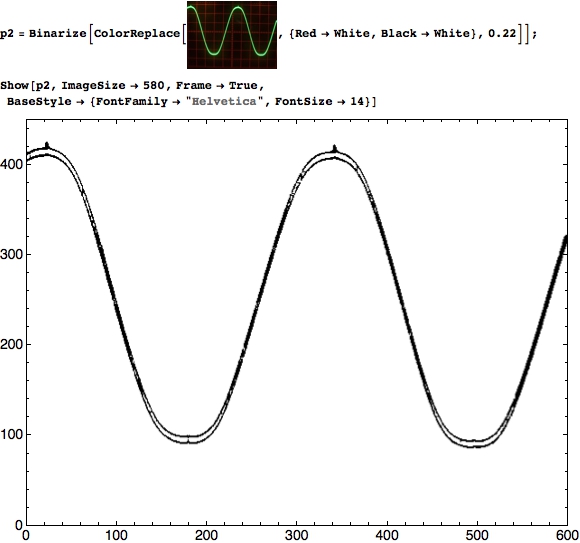
Das Freistellen geht bei den meisten Fotos dieser Art ganz simpel: Einfach die Farben die stören durch Weiß ersetzen, das macht man in Mathematica am bequemsten mit der Funktion ColorReplace. Anschließend noch nach Schwarz/Weiß umwandeln. Das geht am bequemsten mit der Funktion Binarize (die für Problemfälle sehr praktische Brüder hat: Binarize mit Schwellwert oder MorphologicalBinarize). So sieht das dann aus:

Die Optionen ImageSize, BaseStyle und Frame kannst du natürlich weglassen, die sind nur dazu da, das Aussehen für diesen Bericht anzupassen.

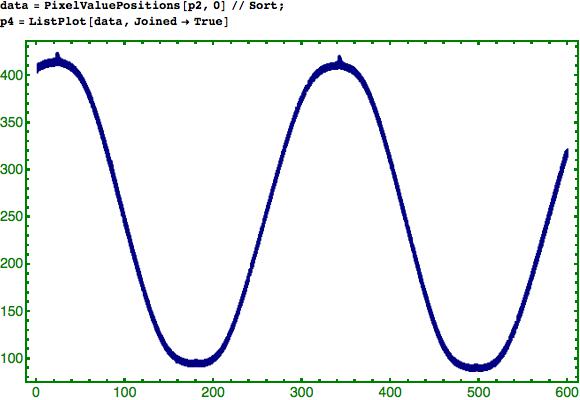
Aus dem Bild müssen wir jetzt nur noch mit dem Befehl PixelValuePositions eine Liste mit den x- und y-Koordinaten der schwarzen Punkte (Farbwert 0) erzeugen und diese nach der x-Koordinate sortieren. Das Sortieren ist glücklicherweise sehr simpel, da der Befehl Sort Pärchen automatisch nach dem ersten Wert sortiert:

Statt mit dem Postfix-Operator // könntest Du Sort natürlich auch einfach direkt als Funktion mit eckigen Klammern anwenden.
Die zweite Zeile könntest du auch weglassen, sie dient nur der optischen Kontrolle.

Vereinzeln

Jetzt gibt es jede x-Koordinate mehrfach und das mit verschiedenen Werten. Damit ich mit den Daten bequem weiterarbeiten kann, möchte ich die Daten in der Form {eindeutiger X-Wert, {y-Wert, y-Wert, y-Wert, … }} haben:

Die zweite Zeile kannst du weglassen, sie dient nur der Ausgabe eines Kontrollwertes, damit du siehst, wie die Daten jetzt aussehen.

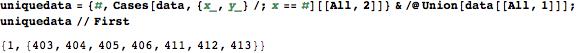[2]

Aufbereiten

Um die Daten abschließend aufzubereiten gibt es eine Reihe von Möglichkeiten, du könntest die Werte mitteln, den Median berechnen, den niedrigsten Wert nehmen und so fort.

Das ist eine entscheidende Stelle, denn der analoge Plot ist natürlich schon sehr breit und in Wirklichkeit (und für Mathematica) noch viel breiter, als man es hier sieht, da wir mit den Augen die dunkleren Grünwerte ziemlich schnell nicht mehr wahrnehmen können, während sie im Datensatz natürlich enthalten sind.

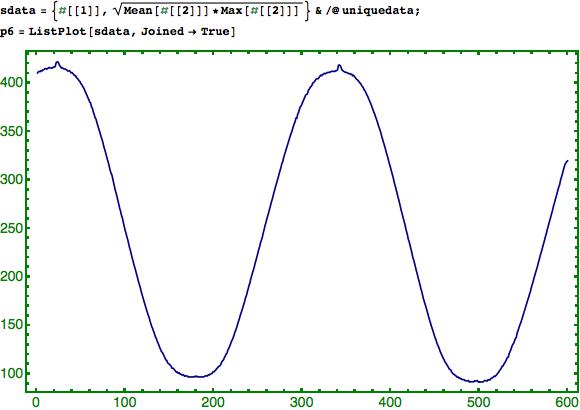
Ich habe hier deswegen den geometrischen Mittelwert aus dem Mittelwert und dem Maximalwert gewählt. Also eine Annäherung an die obere Einhüllende mit einer Glättung durch die Berücksichtigung des normalen Mittelwertes.

Die zweite Zeile kannst du weglassen, sie dient nur dazu die Daten zwecks Kontrolle zu plotten.

[3]

Eine Periode ausschneiden

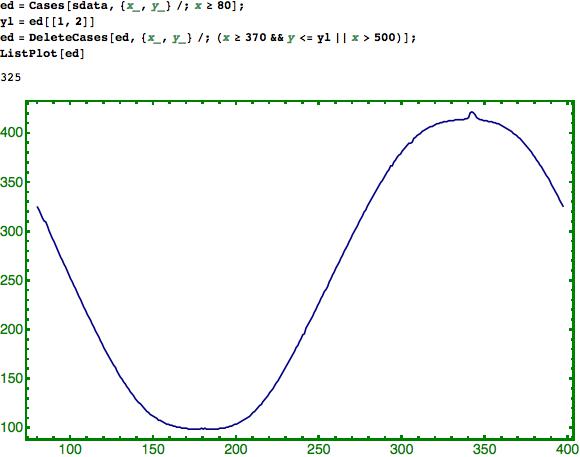
Auf dem Oszilloskop war mehr als eine Periode zu sehen. Für die Weiterverarbeitung mit einem Funktionsgenerator benötige ich aber natürlich nur exakt eine Periode. Deswegen schneide ich jetzt eine Periode aus:

[4]

Auf gleiche Abstände umrechnen

Mein Signalgenerator verlangt eine Liste von y-Werten mit gleichen Abständen.

[5]

Exportieren als CSV

[6]

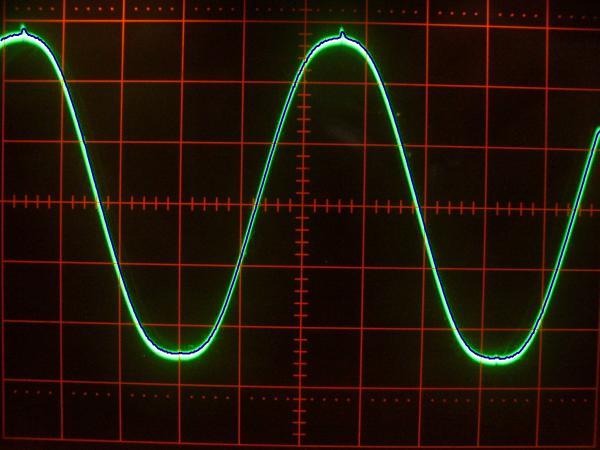
Vergleich der digitalisierten Kurve mit dem Original

[7]

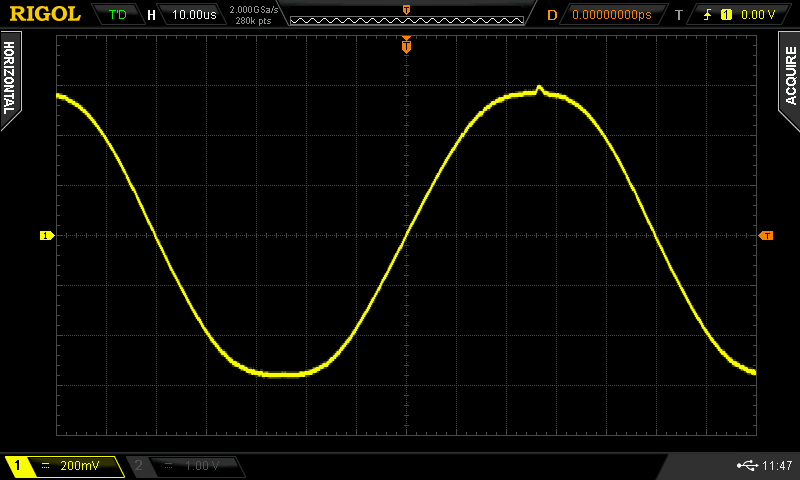
Auf dem Oszilloskop

da muss man jetzt natürlich etwas großzügig sein, vom 600 px per-Hand Foto bis wieder zurück zum Oszilloskop ist es schon ein weiter Weg. Dennoch, so sieht das ganze dann aus (kann durch Klick etwas vergrößert werden):

Source URL: https://drsvanhay.de/abbildungen-und-fotos-digitalisieren-foto-vom-bildschirm-eines-analog-oszilloskopes-nach-csv-mathematica/

---